Twierdzenie o zmianie energii kinetycznej ciała. Podsumowanie lekcji „Energia kinetyczna”

Twierdzenie o energii kinetycznej jest sformułowane w następujący sposób. Suma pracy wszystkich sił (zachowawczych i niezachowawczych) przyłożonych do ciała jest równa przyrostowi jego energii kinetycznej. Korzystając z tego twierdzenia, możemy uogólnić prawo zachowania energii mechanicznej na wypadek system otwarty (nieizolowany).: przyrost całkowita energia mechaniczna system jest równy praca siły zewnętrzne działające na system.

Trajektoria

Trajektoria to wyimaginowana linia opisana przez poruszające się ciało. W zależności od kształtu trajektorii ruchu wyróżnia się krzywoliniową i prostoliniową. Przykłady ruchu krzywoliniowego: ruch ciała rzuconego pod kątem do horyzontu (trajektoria - parabola), ruch punktu materialnego po okręgu.

Tarcie

Zachodzi ono pomiędzy dwoma ciałami w płaszczyźnie styku ich powierzchni i towarzyszy mu rozpraszanie (rozpraszanie) energii. Energia mechaniczna układu, w którym występuje tarcie, może się jedynie zmniejszać. Nauka badająca tarcie nazywa się trybologią. Ustalono doświadczalnie, że maksymalna siła tarcia statycznego i siła tarcia ślizgowego nie zależą od powierzchni styku ciał i są proporcjonalne do normalnej siły nacisku dociskającej powierzchnie do siebie. Nazywa się współczynnikiem proporcjonalności współczynnik tarcia(odpoczynek lub zjeżdżanie).

Trzecie prawo Newtona

Trzecie prawo Newtona jest prawem fizycznym, zgodnie z którym siły oddziaływania między dwoma punktami materialnymi są równe pod względem wielkości, mają przeciwny kierunek i działają wzdłuż linii prostej łączącej te punkty. Podobnie jak inne prawa Newtona, trzecie prawo obowiązuje tylko dla inercyjne układy odniesienia. Krótkie przedstawienie trzeciego prawa: akcja równa się reakcji.

Trzecia prędkość ucieczki

Trzecia prędkość kosmiczna jest minimalna prędkość, niezbędny, aby statek kosmiczny wystrzelony z Ziemi pokonał grawitację Słońca i opuścił Układ Słoneczny. Gdyby Ziemia w chwili wystrzelenia była nieruchoma i nie przyciągała ciała do siebie, wówczas trzecia prędkość kosmiczna wynosiłaby 42 km/s. Biorąc pod uwagę prędkość ruchu orbitalnego Ziemi (30 km/s), trzecia prędkość ucieczki wynosi 42-30 = 12 km/s (przy wystrzeleniu w kierunku ruchu orbitalnego) lub 42+30 = 72 km/s ( przy wystrzeleniu w przeciwnym kierunku). Jeśli uwzględnimy także siłę grawitacji skierowaną w stronę Ziemi, to dla trzeciej prędkości ucieczki otrzymamy wartości od 17 do 73 km/s.

Przyśpieszenie

Przyspieszenie jest wielkością wektorową charakteryzującą prędkość zmian prędkość. W ruchu dowolnym przyspieszenie definiuje się jako stosunek przyrostu prędkości do odpowiedniego okresu czasu. Jeśli skierujemy ten okres czasu na zero, otrzymamy natychmiastowe przyspieszenie. Oznacza to, że przyspieszenie jest pochodną prędkości po czasie. Jeśli weźmie się pod uwagę skończony okres czasu Δt, wówczas przyspieszenie nazywa się średnim. W ruchu krzywoliniowym całkowite przyspieszenie jest sumą styczny (styczny) I normalne przyspieszenie.

Prędkość kątowa

Prędkość kątowa jest wielkością wektorową charakteryzującą ruch obrotowy ciała sztywnego, skierowaną wzdłuż osi obrotu zgodnie z regułą śruby prawoskrętnej. Średnia prędkość kątowa jest liczbowo równa stosunkowi kąta obrotu do odpowiedniego okresu czasu. Biorąc pochodną kąta obrotu po czasie, otrzymujemy chwilową prędkość kątową. Jednostką prędkości kątowej w układzie SI jest rad/s.

Przyspieszenie grawitacyjne

Przyspieszenie swobodnie spadającego ciała to przyspieszenie, z jakim ciało porusza się pod wpływem siły ciężkości. Przyspieszenie swobodnego spadania jest takie samo dla wszystkich ciał, niezależnie od ich szerokie rzesze. Na Ziemi przyspieszenie swobodnie spadającego ciała zależy od wysokości nad poziomem morza oraz od szerokości geograficznej i kierunku w stronę środka Ziemi. Na 45 0 szerokości geograficznej i na poziomie morza przyspieszenie swobodnie spadającego ciała wynosi g = 9,80665 m/s 2 . W problemach edukacyjnych przyjmuje się najczęściej g = 9,81 m/s 2 .

Prawo fizyczne

Prawo fizyczne jest koniecznym, istotnym i stale powtarzającym się powiązaniem zjawisk, procesów i stanów ciał. Znajomość praw fizycznych jest głównym zadaniem nauk fizycznych.

50. Wahadło fizyczne

Wahadło fizyczne - absolutnie sztywne ciało posiadający oś obrotu. W polu grawitacyjnym wahadło fizyczne może oscylować wokół położenia równowagi masa systemów nie można uznać za skoncentrowane w jednym punkcie. Okres drgań wahadła fizycznego zależy od: moment bezwładności ciała i od odległości od osi obrotu do środek masy.

Energia (z greckiego energieia - aktywność)

Energia jest skalarną wielkością fizyczną, która jest ogólną miarą różnych form ruchu materii oraz miarą przejścia ruchu materii z jednej formy do drugiej. Główne rodzaje energii: mechaniczna, wewnętrzna, elektromagnetyczna, chemiczna, grawitacyjna, jądrowa. Niektóre rodzaje energii można w ściśle określonych ilościach przekształcać na inne (patrz także Prawo zachowania i przemiany energii).

Termodynamika i fizyka molekularna

Twierdzenie o energii kinetycznej punktu w postaci różniczkowej

Mnożąc skalarnie obie strony równania ruchu punktu materialnego przez elementarne przemieszczenie punktu, otrzymujemy

lub, ponieważ , wtedy

Wielkość skalarna lub połowa iloczynu masy punktu i kwadratu jego prędkości nazywana jest energią kinetyczną punktu lub siłą życiową punktu.

Ostatnia równość stanowi treść twierdzenia o energii kinetycznej punktu w postaci różniczkowej, które stwierdza: różniczka energii kinetycznej punktu jest równa pracy elementarnej działającej na punkt siły.

Fizyczne znaczenie twierdzenia o energii kinetycznej jest takie, że praca wykonana przez siłę działającą na punkt kumuluje się w nim jako energia kinetyczna ruchu.

Twierdzenie o energii kinetycznej punktu w postaci całkowej

Niech punkt przesunie się z pozycji A do pozycji B, mijając po swojej trajektorii końcowy łuk AB (ryc. 113). Całkowanie równości od A do B:

gdzie są prędkościami punktu w pozycjach A i B, odpowiednio.

Ostatnia równość stanowi treść twierdzenia o energii kinetycznej punktu w postaci całkowej, które głosi, że: zmiana energii kinetycznej punktu w pewnym okresie czasu jest równa pracy wykonanej w tym czasie przez działająca na nią siła.

Otrzymane twierdzenie jest ważne, gdy punkt porusza się pod wpływem dowolnej siły. Jednakże, jak wskazano, aby obliczyć całkowitą pracę siły, w ogólnym przypadku konieczna jest znajomość równań ruchu punktu.

Dlatego twierdzenie o energii kinetycznej, ogólnie rzecz biorąc, nie daje pierwszej całki równań ruchu.

Całka energetyczna

Twierdzenie o energii kinetycznej podaje pierwszą całkę równań ruchu punktu, jeśli całkowitą pracę wykonaną przez siłę można wyznaczyć bez odwoływania się do równań ruchu. To drugie jest możliwe, jak wskazano wcześniej, jeśli siła działająca na punkt należy do pola siłowego. W tym przypadku wystarczy znać jedynie trajektorię punktu. Niech trajektoria punktu będzie jakąś krzywą, wówczas współrzędne jego punktów można wyrazić poprzez łuk trajektorii, a zatem siłę zależną od współrzędnych punktu można wyrazić poprzez

a twierdzenie o energii kinetycznej daje pierwszą całkę postaci

gdzie są łuki trajektorii odpowiadające punktom A i jest rzutem siły na styczną do trajektorii (ryc. 113).

Energia potencjalna i zasada zachowania energii mechanicznej punktu

Szczególnie interesujący jest ruch punktu w polu potencjalnym, ponieważ twierdzenie o energii kinetycznej daje bardzo ważną całkę równań ruchu.

W polu potencjalnym całkowita praca wykonana przez siłę jest równa różnicy między wartościami funkcji siły na końcu i na początku ścieżki:

Dlatego twierdzenie o energii kinetycznej w tym przypadku zapisuje się jako:

Funkcja siły przyjmowana z przeciwnym znakiem nazywa się energią potencjalną punktu i jest oznaczona literą P:

Energię potencjalną, a także funkcję siły określa się do dowolnej stałej, której wartość wyznaczana jest poprzez wybór powierzchni o poziomie zerowym. Suma energii kinetycznej i potencjalnej punktu nazywa się całkowitą energią mechaniczną punktu.

Twierdzenie o energii kinetycznej punktu, jeśli siła należy do pola potencjalnego, zapisuje się jako:

gdzie są wartości energii potencjalnej odpowiadające punktom A i B. Powstałe równanie stanowi treść prawa zachowania energii mechanicznej dla punktu, które stwierdza: podczas poruszania się w polu potencjalnym suma energii kinetycznej i energia potencjalna punktu pozostaje stała.

Ponieważ prawo zachowania energii mechanicznej obowiązuje tylko dla sił należących do pól potencjalnych, siły takiego pola nazywane są konserwatywnymi (od łacińskiego czasownika conservare – zachować), co podkreśla spełnienie sformułowanego prawa w tym przypadku. Należy zauważyć, że jeśli pojęcie energii kinetycznej ma w swojej definicji podstawy fizyczne, to pojęcie energii potencjalnej ich nie ma. Pojęcie energii potencjalnej w pewnym sensie jest wielkością fikcyjną, którą definiuje się tak, aby zmiany jej wartości dokładnie odpowiadały zmianom energii kinetycznej. Wprowadzenie tej wielkości związanej z ruchem ułatwia opis ruchu i przez to odgrywa znaczącą rolę w tzw. energetycznym opisie ruchu, rozwijanym przez mechanikę analityczną. To drugie oznacza znaczenie wprowadzenia tej wartości.

Wynikowa praca wszystkich sił przyłożonych do ciała jest równa zmianie energii kinetycznej ciała.

Twierdzenie to jest prawdziwe nie tylko dla ruchu postępowego ciała sztywnego, ale także w przypadku jego ruchu dowolnego.

Energię kinetyczną posiadają jedynie ciała w ruchu, dlatego nazywa się ją energią ruchu.

§ 8. Siły konserwatywne (potencjalne).

Pole sił konserwatywnych

def.

Siły, których działanie nie zależy od drogi, po której poruszało się ciało, ale zależy jedynie od początkowego i końcowego położenia ciała, nazywane są siłami zachowawczymi (potencjalnymi).

def.

Pole siłowe to obszar przestrzeni, w każdym punkcie którego siła jest przykładana do umieszczonego tam ciała, zmieniając się w sposób naturalny z punktu do punktu w przestrzeni.

def.

Pole, które nie zmienia się w czasie, nazywa się stacjonarnym.

Można udowodnić następujące 3 stwierdzenia

1) Praca wykonana przez siły zachowawcze wzdłuż dowolnej zamkniętej ścieżki jest równa 0.

Dowód:

2) Jednorodne pole sił jest zachowawcze.

def.

Pole nazywamy jednorodnym, jeśli we wszystkich jego punktach siły działające na umieszczone w nim ciało mają tę samą wartość i kierunek.

Dowód:

3) Pole sił centralnych, w którym wielkość siły zależy tylko od odległości od środka, jest zachowawcze.

def.

Pole sił centralnych to pole sił, w którym w każdym punkcie siła skierowana wzdłuż linii przechodzącej przez ten sam stały punkt – środek pola – działa na poruszające się w nim ciało punktowe.

W ogólnym przypadku takie pole sił centralnych nie jest konserwatywne. Jeżeli w polu sił centralnych wielkość siły zależy tylko od odległości do środka pola siłowego (O), tj. , to takie pole jest konserwatywne (potencjalne).

Dowód:

gdzie jest funkcja pierwotna.

§ 9. Energia potencjalna.

Zależność siły od energii potencjalnej

na polu sił konserwatywnych

Wybierzmy początek współrzędnych jako pole sił zachowawczych, tj.

Energia potencjalna ciała w polu sił zachowawczych. Funkcja ta jest określona jednoznacznie (zależy tylko od współrzędnych), ponieważ praca sił konserwatywnych nie zależy od rodzaju ścieżki.

Znajdźmy połączenie w polu sił zachowawczych podczas przenoszenia ciała z punktu 1 do punktu 2.

Praca sił zachowawczych jest równa zmianie energii potencjalnej o przeciwnym znaku.

Energia potencjalna ciała pola sił zachowawczych to energia wynikająca z obecności pola siłowego, która powstaje w wyniku pewnego oddziaływania danego ciała z ciałem zewnętrznym (ciałami), które, jak mówią, tworzy pole siłowe.

Energia potencjalna pola sił zachowawczych charakteryzuje zdolność ciała do wykonania pracy i jest liczbowo równa pracy sił zachowawczych, aby przesunąć ciało do początku współrzędnych (lub do punktu o zerowej energii). Zależy to od wyboru poziomu zerowego i może być ujemne. W każdym razie, a zatem także w przypadku pracy elementarnej, tj. lub , gdzie jest rzutem siły na kierunek ruchu lub elementarne przemieszczenie. Stąd, . Ponieważ możemy poruszyć ciałem w dowolnym kierunku, to jest to prawdą dla dowolnego kierunku. Rzut siły zachowawczej na dowolny kierunek jest równy pochodnej energii potencjalnej w tym kierunku o przeciwnym znaku.

Uwzględniając rozwinięcie wektorów i ze względu na bazę , otrzymujemy to

Natomiast z analizy matematycznej wiadomo, że całkowita różniczka funkcji kilku zmiennych jest równa sumie iloczynów pochodnych cząstkowych po argumentach i różniczkach argumentów, tj. , co oznacza z relacji, którą otrzymujemy

Aby zapisać te relacje w sposób bardziej zwięzły, można skorzystać z koncepcji gradientu funkcji.

def.

Gradient jakiejś skalarnej funkcji współrzędnych jest wektorem o współrzędnych równych odpowiednim pochodnym cząstkowym tej funkcji.

W naszym przypadku

def.

Powierzchnia ekwipotencjalna to geometryczne miejsce punktów w polu sił zachowawczych, których wartości energii potencjalnej są takie same, tj. .

Ponieważ z definicji powierzchni ekwipotencjalnej wynika, że dla punktów na tej powierzchni , jako pochodna stałej, zatem .

Zatem siła zachowawcza jest zawsze prostopadła do powierzchni ekwipotencjalnej i skierowana jest w kierunku spadku energii potencjalnej. (P1 > P2 > P3).

§ 10. Energia potencjalna oddziaływania.

Konserwatywne układy mechaniczne

Rozważmy układ dwóch oddziałujących ze sobą cząstek. Niech siły ich oddziaływania będą centralne, a wielkość siły zależy od odległości między cząstkami (takimi siłami są siły grawitacyjne i elektryczne siły Coulomba). Jest oczywiste, że siły oddziaływania między dwiema cząstkami mają charakter wewnętrzny.

Uwzględniając trzecie prawo Newtona (), otrzymujemy, tj. praca sił wewnętrznych oddziaływania między dwiema cząstkami jest zdeterminowana zmianą odległości między nimi.

Tę samą pracę wykonanoby, gdyby pierwsza cząstka znajdowała się w spoczynku w początku układu współrzędnych, a druga otrzymała przemieszczenie równe przyrostowi wektora jej promienia, tj. pracę wykonaną przez siły wewnętrzne można obliczyć, rozważając, że jedna cząstka jest nieruchoma, a drugi porusza się w polu sił centralnych, których wielkość jest jednoznacznie określona przez odległość między cząstkami. W §8 wykazaliśmy, że pole takich sił (czyli pole sił centralnych, w którym wielkość siły zależy jedynie od odległości od środka) jest zachowawcze, co oznacza, że ich pracę można uznać za zmniejszenie energia potencjalna (zdefiniowana zgodnie z §9 dla pola sił zachowawczych).

W rozpatrywanym przypadku energia ta powstaje w wyniku oddziaływania dwóch cząstek tworzących układ zamknięty. Nazywa się to energią potencjalną interakcji (lub wzajemną energią potencjalną). Zależy to również od wyboru poziomu zerowego i może być ujemne.

def.

Układ mechaniczny ciał sztywnych, pomiędzy którymi siły wewnętrzne są zachowawcze, nazywany jest konserwatywnym układem mechanicznym.

Można wykazać, że potencjalna energia interakcji konserwatywnego układu cząstek N składa się z potencjalnych energii interakcji cząstek zebranych parami, które można sobie wyobrazić.

Gdzie jest energia potencjalna oddziaływania między dwiema cząstkami i-tą i j-tą. Wskaźniki i i j w sumie przyjmują niezależne wartości 1,2,3, ..., N. Biorąc pod uwagę, że ta sama energia potencjalna oddziaływania i-tej i j-tej cząstki ze sobą, to przy sumowaniu , energia zostanie pomnożona przez 2, w wyniku czego przed kwotą pojawi się współczynnik. Ogólnie rzecz biorąc, potencjalna energia interakcji układu N cząstek będzie zależeć od położenia lub współrzędnych wszystkich cząstek. Łatwo zauważyć, że energia potencjalna cząstki w polu sił zachowawczych jest rodzajem energii potencjalnej oddziaływania układu cząstek, ponieważ pole siłowe jest wynikiem wzajemnego oddziaływania ciał.

§ 11. Prawo zachowania energii w mechanice.

Niech ciało sztywne porusza się translacyjnie pod działaniem sił konserwatywnych i niezachowawczych, tj. przypadek ogólny. Wtedy wypadkowa wszystkich sił działających na ciało wynosi . Praca wypadkowej wszystkich sił w tym przypadku.

Z twierdzenia o energii kinetycznej i biorąc to pod uwagę, otrzymujemy

Całkowita energia mechaniczna ciała

Jeśli więc. Jest to matematyczne przedstawienie prawa zachowania energii w mechanice dla pojedynczego ciała.

Sformułowanie prawa zachowania energii:

Całkowita energia mechaniczna ciała nie zmienia się, gdy nie działają siły niezachowawcze.

Dla mechanicznego układu cząstek N łatwo wykazać, że (*) ma miejsce.

Naraz

Pierwsza suma to całkowita energia kinetyczna układu cząstek.

Druga to całkowita energia potencjalna cząstek w zewnętrznym polu sił zachowawczych

Trzecia to energia potencjalna interakcji cząstek układu ze sobą.

Druga i trzecia suma reprezentują całkowitą energię potencjalną układu.

Praca sił niezachowawczych składa się z dwóch terminów, reprezentujących pracę sił wewnętrznych i zewnętrznych niezachowawczych.

Podobnie jak w przypadku ruchu pojedynczego ciała, dla układu mechanicznego N ciał, jeżeli , to , a zasada zachowania energii w ogólnym przypadku układu mechanicznego stwierdza:

Całkowita energia mechaniczna układu cząstek, na który działają jedynie siły zachowawcze, zostaje zachowana.

Zatem w obecności sił niezachowawczych całkowita energia mechaniczna nie jest zachowana.

Siłami niezachowawczymi są np. siła tarcia, siła oporu i inne siły, których działanie powoduje odcynowanie energii (przemianę energii mechanicznej na ciepło).

Siły prowadzące do desynizacji nazywane są dessynatywnymi. Niektóre siły niekoniecznie mają charakter docelowy.

Prawo zachowania energii jest uniwersalne i dotyczy nie tylko zjawisk mechanicznych, ale także wszystkich procesów zachodzących w przyrodzie. Całkowita ilość energii w izolowanym układzie ciał i pól zawsze pozostaje stała. Energia może przemieszczać się tylko z jednej formy do drugiej.

Biorąc pod uwagę tę równość

Jeśli potrzebujesz dodatkowych materiałów na ten temat lub nie znalazłeś tego czego szukałeś, polecamy skorzystać z wyszukiwarki w naszej bazie dzieł:

Co zrobimy z otrzymanym materiałem:

Jeśli ten materiał był dla Ciebie przydatny, możesz zapisać go na swojej stronie w sieciach społecznościowych:

Pogląd: ten artykuł został przeczytany 48440 razy

PDF Wybierz język... Rosyjski Ukraiński Angielski

Krótki przegląd

Całość materiału pobiera się powyżej, po wybraniu języka

Dwa przypadki transformacji ruchu mechanicznego punktu materialnego lub układu punktów:

ruch mechaniczny jest przenoszony z jednego układu mechanicznego na drugi jako ruch mechaniczny;
ruch mechaniczny zamienia się w inną formę ruchu materii (w postaci energii potencjalnej, ciepła, elektryczności itp.).

Gdy rozważa się przekształcenie ruchu mechanicznego bez jego przejścia w inną formę ruchu, miarą ruchu mechanicznego jest wektor pędu punktu materialnego lub układu mechanicznego. Miarą siły jest w tym przypadku wektor impulsu siły.

Kiedy ruch mechaniczny zamienia się w inną formę ruchu materii, energia kinetyczna punktu materialnego lub układu mechanicznego działa jako miara ruchu mechanicznego. Miarą działania siły przy przekształcaniu ruchu mechanicznego w inną formę ruchu jest praca siły

Energia kinetyczna

Energia kinetyczna to zdolność organizmu do pokonywania przeszkód podczas ruchu.

Energia kinetyczna punktu materialnego

Energia kinetyczna punktu materialnego jest wielkością skalarną równą połowie iloczynu masy punktu i kwadratu jego prędkości.

Energia kinetyczna:

charakteryzuje zarówno ruchy translacyjne, jak i obrotowe;
nie zależy od kierunku ruchu punktów układu i nie charakteryzuje zmian w tych kierunkach;
charakteryzuje działanie sił wewnętrznych i zewnętrznych.

Energia kinetyczna układu mechanicznego

Energia kinetyczna układu jest równa sumie energii kinetycznych ciał układu. Energia kinetyczna zależy od rodzaju ruchu ciał układu.

Wyznaczanie energii kinetycznej ciała stałego dla różnych rodzajów ruchu.

Energia kinetyczna ruchu postępowego
Podczas ruchu postępowego energia kinetyczna ciała jest równa T=M V 2 /2.

Miarą bezwładności ciała podczas ruchu postępowego jest masa.

Energia kinetyczna ruchu obrotowego ciała

Podczas ruchu obrotowego ciała energia kinetyczna jest równa połowie iloczynu momentu bezwładności ciała względem osi obrotu i kwadratu jego prędkości kątowej.

Miarą bezwładności ciała podczas ruchu obrotowego jest moment bezwładności.

Energia kinetyczna ciała nie zależy od kierunku obrotu ciała.

Energia kinetyczna ruchu płasko-równoległego ciała

Przy ruchu płasko-równoległym ciała energia kinetyczna jest równa

Praca siły

Praca siły charakteryzuje działanie siły na ciało podczas pewnego ruchu i określa zmianę modułu prędkości poruszającego się punktu.

Elementarna praca siły

Elementarną pracę siły definiuje się jako wielkość skalarną równą iloczynowi rzutu siły na styczną do trajektorii, skierowaną w kierunku ruchu punktu, i nieskończenie małego przemieszczenia punktu, skierowanego wzdłuż tej tangens.

Praca wykonana przez siłę przy przemieszczeniu końcowym

Praca wykonana przez siłę przy przemieszczeniu końcowym jest równa sumie jej pracy na przekrojach elementarnych.

Praca siły na przemieszczenie końcowe M 1 M 0 jest równa całce pracy elementarnej wzdłuż tego przemieszczenia.

Działanie siły na przemieszczenie M 1 M 2 jest przedstawione przez obszar figury ograniczony osią odciętej, krzywą i rzędnymi odpowiadającymi punktom M 1 i M 0.

Jednostką miary pracy siły i energii kinetycznej w układzie SI jest 1 (J).

Twierdzenia o działaniu siły

Twierdzenie 1. Praca wykonana przez wypadkową siłę przy pewnym przemieszczeniu jest równa algebraicznej sumie pracy wykonanej przez siły składowe przy tym samym przemieszczeniu.

Twierdzenie 2. Praca wykonana przez stałą siłę nad wynikowym przemieszczeniem jest równa sumie algebraicznej pracy wykonanej przez tę siłę nad przemieszczeniami składowych.

Moc

Moc jest wielkością określającą pracę siły w jednostce czasu.

Jednostką miary mocy jest 1W = 1 J/s.

Przypadki wyznaczania pracy sił

Praca sił wewnętrznych

Suma pracy sił wewnętrznych ciała sztywnego podczas dowolnego ruchu wynosi zero.

Praca grawitacji

Praca siły sprężystej

Praca siły tarcia

Praca sił przyłożonych do obracającego się ciała

Elementarna praca sił przyłożonych do ciała sztywnego obracającego się wokół ustalonej osi jest równa iloczynowi głównego momentu sił zewnętrznych względem osi obrotu i przyrostu kąta obrotu.

Opór toczenia

W strefie styku nieruchomego cylindra z płaszczyzną następuje lokalne odkształcenie ściskania styku, naprężenia rozkładają się zgodnie z prawem eliptycznym, a linia działania wypadkowej N tych naprężeń pokrywa się z linią działania obciążenia siła działająca na cylinder Q. Kiedy cylinder się toczy, rozkład obciążenia staje się asymetryczny, a maksimum jest przesunięte w kierunku ruchu. Wynikowy N jest przesunięty o wielkość k – ramię siły tarcia tocznego, zwane także współczynnikiem tarcia tocznego i ma wymiar długości (cm)

Twierdzenie o zmianie energii kinetycznej punktu materialnego

Zmiana energii kinetycznej punktu materialnego przy pewnym przemieszczeniu jest równa sumie algebraicznej wszystkich sił działających na punkt przy tym samym przemieszczeniu.

Twierdzenie o zmianie energii kinetycznej układu mechanicznego

Zmiana energii kinetycznej układu mechanicznego przy pewnym przemieszczeniu jest równa sumie algebraicznej sił wewnętrznych i zewnętrznych działających na punkty materialne układu przy tym samym przemieszczeniu.

Twierdzenie o zmianie energii kinetycznej ciała stałego

Zmiana energii kinetycznej ciała sztywnego (układu niezmienionego) przy określonym przemieszczeniu jest równa sumie sił zewnętrznych działających na punkty układu przy tym samym przemieszczeniu.

Efektywność

Siły działające w mechanizmach

Siły i pary sił (momenty) działające na mechanizm lub maszynę można podzielić na grupy:

1. Siły napędowe i momenty wykonujące pracę dodatnią (przyłożone do ogniw napędowych, np. ciśnienie gazu na tłoku w silniku spalinowym).

2. Siły i momenty oporu wykonujące pracę ujemną:

opory użyteczne (wykonują pracę wymaganą od maszyny i przykładane są do ogniw napędzanych, np. opór ładunku podnoszonego przez maszynę),
siły oporu (na przykład siły tarcia, opór powietrza itp.).

3. Siły ciężkości i siły sprężystości sprężyn (zarówno praca dodatnia, jak i ujemna, przy czym praca w pełnym cyklu wynosi zero).

4. Siły i momenty przyłożone do ciała lub stojaka z zewnątrz (reakcja fundamentu itp.), które nie wykonują pracy.

5. Siły oddziaływania pomiędzy ogniwami działającymi w parach kinematycznych.

6. Siły bezwładności ogniw, wywołane masą i ruchem ogniw z przyspieszeniem, mogą wykonywać pracę dodatnią, ujemną i nie wykonywać pracy.

Praca sił w mechanizmach

W stanie ustalonym pracy maszyny jej energia kinetyczna nie ulega zmianie, a suma pracy przyłożonych do niej sił napędowych i sił oporu jest równa zeru.

Praca włożona w wprawienie maszyny w ruch jest poświęcona pokonywaniu pożytecznych i szkodliwych oporów.

Sprawność mechanizmu

Sprawność mechaniczna w ruchu ustalonym jest równa stosunkowi pracy użytecznej maszyny do pracy włożonej w jej wprawienie w ruch:

Elementy maszyn można łączyć szeregowo, równolegle i mieszanie.

Wydajność w połączeniu szeregowym

Gdy mechanizmy są połączone szeregowo, ogólna wydajność jest mniejsza niż najniższa wydajność pojedynczego mechanizmu.

Wydajność w połączeniu równoległym

Gdy mechanizmy są połączone równolegle, ogólna sprawność jest większa od najniższej i mniejsza od najwyższej sprawności pojedynczego mechanizmu.

Format: pdf

Język: rosyjski, ukraiński

Przykład obliczeń koła zębatego czołowego
Przykład obliczenia koła zębatego czołowego. Dokonano doboru materiału, obliczenia dopuszczalnych naprężeń, obliczenia wytrzymałości stykowej i zginającej.

Przykład rozwiązania problemu zginania belki
W przykładzie skonstruowano wykresy sił poprzecznych i momentów zginających, znaleziono niebezpieczny przekrój i wybrano dwuteownik. W zadaniu dokonano analizy konstrukcji diagramów wykorzystując zależności różniczkowe oraz przeprowadzono analizę porównawczą różnych przekrojów belki.

Przykład rozwiązania problemu skręcania wału
Zadanie polega na zbadaniu wytrzymałości wału stalowego przy zadanej średnicy, materiale i dopuszczalnym naprężeniu. Podczas rozwiązywania konstruowane są wykresy momentów obrotowych, naprężeń ścinających i kątów skręcenia. Ciężar własny wału nie jest brany pod uwagę

Przykład rozwiązania problemu rozciągania-ściskania pręta
Zadanie polega na badaniu wytrzymałości pręta stalowego przy określonych naprężeniach dopuszczalnych. Podczas rozwiązywania konstruowane są wykresy sił podłużnych, naprężeń normalnych i przemieszczeń. Ciężar własny wędki nie jest brany pod uwagę

Zastosowanie twierdzenia o zachowaniu energii kinetycznej
Przykład rozwiązania problemu z wykorzystaniem twierdzenia o zachowaniu energii kinetycznej układu mechanicznego

Energia jest skalarną wielkością fizyczną będącą ujednoliconą miarą różnych form ruchu materii oraz miarą przejścia ruchu materii z jednej formy do drugiej.

Aby scharakteryzować różne formy ruchu materii, wprowadza się odpowiednie rodzaje energii, na przykład: mechaniczną, wewnętrzną, energię oddziaływań elektrostatycznych, wewnątrzjądrowych itp.

Energia podlega prawu zachowania, które jest jednym z najważniejszych praw natury.

Energia mechaniczna E charakteryzuje ruch i wzajemne oddziaływanie ciał oraz jest funkcją prędkości i względnego położenia ciał. Jest równa sumie energii kinetycznej i potencjalnej.

Energia kinetyczna

Rozważmy przypadek, gdy ciało ma masę M istnieje stała siła \(~\vec F\) (może być wypadkową kilku sił) i wektory siły \(~\vec F\) i przemieszczenia \(~\vec s\) są skierowane wzdłuż jednego linię prostą w jednym kierunku. W tym przypadku pracę wykonaną przez siłę można zdefiniować jako A = F∙S. Moduł siły zgodnie z drugim prawem Newtona jest równy F = m∙a i moduł przemieszczenia S w równomiernie przyspieszonym ruchu prostoliniowym jest powiązany z modułami początkowymi υ 1 i ostateczny υ 2 prędkości i przyspieszenia A wyrażenie \(~s = \frac(\upsilon^2_2 - \upsilon^2_1)(2a)\) .

Stąd zabieramy się do pracy

\(~A = F \cdot s = m \cdot a \cdot \frac(\upsilon^2_2 - \upsilon^2_1)(2a) = \frac(m \cdot \upsilon^2_2)(2) - \frac (m \cdot \upsilon^2_1)(2)\) . (1)

Wielkość fizyczna równa połowie iloczynu masy ciała i kwadratu jego prędkości nazywa się energia kinetyczna ciała.

Energię kinetyczną reprezentuje litera mi k.

\(~E_k = \frac(m \cdot \upsilon^2)(2)\) . (2)

Wówczas równość (1) można zapisać następująco:

\(~A = E_(k2) - E_(k1)\) . (3)

Twierdzenie o energii kinetycznej

praca wypadkowych sił przyłożonych do ciała jest równa zmianie energii kinetycznej ciała.

Ponieważ zmiana energii kinetycznej jest równa pracy siły (3), energię kinetyczną ciała wyraża się w tych samych jednostkach co praca, czyli w dżulach.

Jeżeli początkowa prędkość ruchu ciała masowego M wynosi zero, a ciało zwiększa prędkość do tej wartości υ , to praca wykonana przez tę siłę jest równa końcowej wartości energii kinetycznej ciała:

\(~A = E_(k2) - E_(k1)= \frac(m \cdot \upsilon^2)(2) - 0 = \frac(m \cdot \upsilon^2)(2)\) . (4)

Fizyczne znaczenie energii kinetycznej

Energia kinetyczna ciała poruszającego się z prędkością v pokazuje, jaką pracę musi wykonać siła działająca na ciało w spoczynku, aby nadać mu tę prędkość.

Energia potencjalna

Energia potencjalna jest energią oddziaływania pomiędzy ciałami.

Energia potencjalna ciała uniesionego nad Ziemią to energia oddziaływania ciała z Ziemią za pomocą sił grawitacyjnych. Energia potencjalna ciała odkształconego sprężyście to energia oddziaływania poszczególnych części ciała na siebie za pomocą sił sprężystych.

Potencjał są nazywane wytrzymałość, którego praca zależy jedynie od początkowego i końcowego położenia poruszającego się punktu materialnego lub ciała i nie zależy od kształtu trajektorii.

Na trajektorii zamkniętej praca wykonana przez siłę potencjalną jest zawsze równa zeru. Potencjalne siły obejmują siły grawitacyjne, siły sprężystości, siły elektrostatyczne i niektóre inne.

Uprawnienie, których praca zależy od kształtu trajektorii, nazywane są niepotencjalny. Kiedy punkt materialny lub ciało porusza się po zamkniętej trajektorii, praca wykonana przez siłę niepotencjalną nie jest równa zeru.

Energia potencjalna oddziaływania ciała z Ziemią

Znajdźmy pracę wykonaną przez grawitację F t podczas przesuwania ciała o masie M pionowo w dół z pewnej wysokości H 1 nad powierzchnią Ziemi na wysokość H 2 (ryc. 1). Jeśli różnica H 1 – H 2 jest znikomy w porównaniu do odległości do środka Ziemi, a następnie siły ciężkości F t podczas ruchu ciała można uznać za stałe i równe mg.

Ponieważ przemieszczenie pokrywa się w kierunku z wektorem grawitacji, praca wykonana przez grawitację jest równa

\(~A = F \cdot s = m \cdot g \cdot (h_1 - h_2)\) . (5)

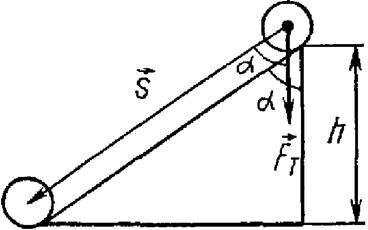
Rozważmy teraz ruch ciała po pochyłej płaszczyźnie. Podczas przesuwania ciała w dół po nachylonej płaszczyźnie (ryc. 2) siła ciężkości F t = m∙g działa

\(~A = m \cdot g \cdot s \cdot \cos \alpha = m \cdot g \cdot h\) , (6)

Gdzie H– wysokość płaszczyzny pochyłej, S– moduł przemieszczenia równy długości pochyłej płaszczyzny.

Ruch ciała z punktu W rzeczowy Z po dowolnej trajektorii (ryc. 3) można sobie wyobrazić jako składające się z ruchów wzdłuż odcinków pochyłych płaszczyzn o różnych wysokościach H’, H'' itp. Praca A grawitacja na całej długości W V Z równa sumie pracy na poszczególnych odcinkach trasy:

\(~A = m \cdot g \cdot h" + m \cdot g \cdot h"" + \ldots + m \cdot g \cdot h^n = m \cdot g \cdot (h" + h"" + \ldots + h^n) = m \cdot g \cdot (h_1 - h_2)\), (7)

Gdzie H 1 i H 2 – wysokości od powierzchni Ziemi, na których znajdują się odpowiednio punkty W I Z.

Z równości (7) wynika, że praca grawitacji nie zależy od toru ruchu ciała i jest zawsze równa iloczynowi modułu grawitacji i różnicy wysokości w położeniu początkowym i końcowym.

Podczas ruchu w dół praca grawitacji jest dodatnia, podczas ruchu w górę jest ujemna. Praca wykonana przez grawitację na zamkniętej trajektorii wynosi zero.

Równość (7) można przedstawić w następujący sposób:

\(~A = - (m \cdot g \cdot h_2 - m \cdot g \cdot h_1)\) . (8)

Nazywa się wielkość fizyczną równą iloczynowi masy ciała przez moduł przyspieszenia swobodnego spadania i wysokość, na jaką ciało unosi się nad powierzchnią Ziemi energia potencjalna interakcja pomiędzy ciałem a Ziemią.

Praca wykonana przez grawitację podczas przemieszczania ciała o masie M z punktu położonego na dużej wysokości H 2, do punktu znajdującego się na wysokości H 1 z powierzchni Ziemi, wzdłuż dowolnej trajektorii, jest równa zmianie energii potencjalnej oddziaływania ciała z Ziemią, przyjętej ze znakiem przeciwnym.

\(~A = - (E_(p2) - E_(p1))\) . (9)

Energia potencjalna jest oznaczona literą mi P.

Wartość energii potencjalnej ciała wzniesionego nad Ziemię zależy od wyboru poziomu zerowego, czyli wysokości, na której przyjmuje się, że energia potencjalna wynosi zero. Zwykle przyjmuje się, że energia potencjalna ciała na powierzchni Ziemi wynosi zero.

Przy tym wyborze poziomu zerowego, energia potencjalna mi p ciała znajdującego się na wysokości H nad powierzchnią Ziemi, równy iloczynowi masy m ciała przez moduł przyspieszenia grawitacyjnego G i dystans H to z powierzchni Ziemi:

\(~E_p = m \cdot g \cdot h\) . (10)

Fizyczne znaczenie energii potencjalnej oddziaływania ciała z Ziemią

energia potencjalna ciała, na które działa grawitacja, jest równa pracy wykonanej przez grawitację podczas przemieszczania ciała do poziomu zerowego.

W przeciwieństwie do energii kinetycznej ruchu postępowego, która może przyjmować tylko wartości dodatnie, energia potencjalna ciała może być zarówno dodatnia, jak i ujemna. Masa ciała M, położony na wysokości H, Gdzie H < H 0 (H 0 – wysokość zerowa), ma ujemną energię potencjalną:

\(~E_p = -m \cdot g \cdot h\) .

Energia potencjalna oddziaływania grawitacyjnego

Energia potencjalna oddziaływania grawitacyjnego układu dwóch punktów materialnych z masami M I M, położony w pewnej odległości R jedno od drugiego jest równe

\(~E_p = G \cdot \frac(M \cdot m)(r)\) . (11)

Gdzie G jest stałą grawitacji i zerem energii potencjalnej odniesienia ( mi p = 0) przyjęte o godz R = ∞.

Energia potencjalna oddziaływania grawitacyjnego ciała z masą M z Ziemią, gdzie H– wysokość ciała nad powierzchnią ziemi, M e – masa Ziemi, R e jest promieniem Ziemi i wybiera się zero odczytu energii potencjalnej H = 0.

\(~E_e = G \cdot \frac(M_e \cdot m \cdot h)(R_e \cdot (R_e +h))\) . (12)

Pod tym samym warunkiem wyboru zerowego odniesienia, energia potencjalna oddziaływania grawitacyjnego ciała z masą M z Ziemią na małych wysokościach H (H « R e) równe

\(~E_p = m \cdot g \cdot h\) ,

gdzie \(~g = G \cdot \frac(M_e)(R^2_e)\) jest modułem przyspieszenia grawitacyjnego w pobliżu powierzchni Ziemi.

Energia potencjalna ciała odkształconego sprężyście

Obliczmy pracę wykonaną przez siłę sprężystości, gdy odkształcenie (wydłużenie) sprężyny zmieni się od pewnej wartości początkowej X 1 do wartości końcowej X 2 (ryc. 4, b, c).

Siła sprężystości zmienia się wraz z odkształceniem sprężyny. Aby obliczyć pracę wykonaną przez siłę sprężystości, można przyjąć średnią wartość modułu siły (ponieważ siła sprężystości zależy liniowo od X) i pomnóż przez moduł przemieszczenia:

\(~A = F_(upr-cp) \cdot (x_1 - x_2)\) , (13)

gdzie \(~F_(upr-cp) = k \cdot \frac(x_1 - x_2)(2)\) . Stąd

\(~A = k \cdot \frac(x_1 - x_2)(2) \cdot (x_1 - x_2) = k \cdot \frac(x^2_1 - x^2_2)(2)\) lub \(~A = -\left(\frac(k \cdot x^2_2)(2) - \frac(k \cdot x^2_1)(2) \right)\) . (14)

Nazywa się wielkość fizyczną równą połowie iloczynu sztywności ciała przez kwadrat jego odkształcenia energia potencjalna ciało odkształcone sprężyście:

\(~E_p = \frac(k \cdot x^2)(2)\) . (15)

Ze wzorów (14) i (15) wynika, że praca siły sprężystej jest równa zmianie energii potencjalnej ciała odkształconego sprężyście, przyjętej ze znakiem przeciwnym:

\(~A = -(E_(p2) - E_(p1))\) . (16)

Jeśli X 2 = 0 i X 1 = X, zatem, jak widać ze wzorów (14) i (15),

\(~E_p = A\) .

Fizyczne znaczenie energii potencjalnej ciała odkształconego

energia potencjalna ciała odkształconego sprężyście jest równa pracy wykonanej przez siłę sprężystości, gdy ciało przechodzi do stanu, w którym odkształcenie wynosi zero.

Energia potencjalna charakteryzuje ciała oddziałujące, a energia kinetyczna charakteryzuje ciała poruszające się. Zarówno energia potencjalna, jak i kinetyczna zmieniają się jedynie w wyniku takiego oddziaływania ciał, w którym siły działające na ciała wykonują pracę różną od zera. Rozważmy kwestię zmian energii podczas oddziaływań ciał tworzących układ zamknięty.

System zamknięty- jest to układ, na który nie działają siły zewnętrzne lub działanie tych sił jest kompensowane. Jeżeli kilka ciał oddziałuje ze sobą tylko za pomocą sił grawitacyjnych i sił sprężystych i nie działają na nie żadne siły zewnętrzne, to dla wszelkich interakcji ciał praca sił sprężystych lub sił grawitacyjnych jest równa zmianie energii potencjalnej ciał , wzięte z przeciwnym znakiem:

\(~A = -(E_(p2) - E_(p1))\) . (17)

Zgodnie z twierdzeniem o energii kinetycznej praca wykonana przez te same siły jest równa zmianie energii kinetycznej:

\(~A = E_(k2) - E_(k1)\) . (18)

Z porównania równości (17) i (18) wynika, że zmiana energii kinetycznej ciał w układzie zamkniętym jest w wartości bezwzględnej równa zmianie energii potencjalnej układu ciał i ma przeciwny znak:

\(~E_(k2) - E_(k1) = -(E_(p2) - E_(p1))\) lub \(~E_(k1) + E_(p1) = E_(k2) + E_(p2) \) . (19)

Prawo zachowania energii w procesach mechanicznych:

suma energii kinetycznej i potencjalnej ciał tworzących układ zamknięty i oddziałujących ze sobą siłami grawitacji i sprężystości pozostaje stała.

Nazywa się sumą energii kinetycznej i potencjalnej ciał całkowita energia mechaniczna.

Przeprowadźmy prosty eksperyment. Rzućmy stalową kulę w górę. Podając prędkość początkową υ inch, nadamy mu energię kinetyczną, dlatego zacznie rosnąć w górę. Działanie grawitacji prowadzi do zmniejszenia prędkości piłki, a co za tym idzie, jej energii kinetycznej. Ale piłka wznosi się coraz wyżej i zdobywa coraz więcej energii potencjalnej ( mi p = m∙g∙h). Zatem energia kinetyczna nie znika bez śladu, ale zamienia się w energię potencjalną.

W momencie osiągnięcia najwyższego punktu trajektorii ( υ = 0) piłka jest całkowicie pozbawiona energii kinetycznej ( mi k = 0), ale jednocześnie jego energia potencjalna staje się maksymalna. Następnie piłka zmienia kierunek i porusza się w dół ze zwiększającą się prędkością. Teraz energia potencjalna jest zamieniana z powrotem na energię kinetyczną.

Ujawnia prawo zachowania energii znaczenie fizyczne koncepcje praca:

praca sił grawitacyjnych i sprężystych jest z jednej strony równa wzrostowi energii kinetycznej, a z drugiej strony zmniejszeniu energii potencjalnej ciał. Dlatego praca jest równa energii przetworzonej z jednego rodzaju na drugi.

Prawo zmiany energii mechanicznej

Jeżeli układ oddziałujących ze sobą ciał nie jest zamknięty, to jego energia mechaniczna nie jest zachowana. Zmiana energii mechanicznej takiego układu jest równa działaniu sił zewnętrznych:

\(~A_(vn) = \Delta E = E - E_0\) . (20)

Gdzie mi I mi 0 – sumaryczna energia mechaniczna układu odpowiednio w stanie końcowym i początkowym.

Przykładem takiego układu jest układ, w którym wraz z siłami potencjalnymi działają siły niepotencjalne. Siły niepotencjalne obejmują siły tarcia. W większości przypadków, gdy kąt pomiędzy siłą tarcia F R ciało jest π radianów, praca wykonana przez siłę tarcia jest ujemna i równa

\(~A_(tr) = -F_(tr) \cdot s_(12)\) ,

Gdzie S 12 – ścieżka ciała pomiędzy punktami 1 i 2.

Siły tarcia podczas ruchu układu zmniejszają jego energię kinetyczną. W rezultacie energia mechaniczna zamkniętego układu niekonserwatywnego zawsze maleje, zamieniając się w energię niemechanicznych form ruchu.

Przykładowo samochód poruszający się po poziomym odcinku drogi po wyłączeniu silnika pokonuje pewien dystans i zatrzymuje się pod wpływem sił tarcia. Energia kinetyczna ruchu do przodu samochodu stała się równa zeru, a energia potencjalna nie wzrosła. Kiedy samochód hamował, klocki hamulcowe, opony samochodowe i asfalt nagrzewały się. W rezultacie w wyniku działania sił tarcia energia kinetyczna samochodu nie zanikła, lecz zamieniła się w energię wewnętrzną ruchu termicznego cząsteczek.

Prawo zachowania i przemiany energii

W każdej interakcji fizycznej energia ulega przemianie z jednej formy w drugą.

Czasami kąt pomiędzy siłą tarcia F tr i przemieszczenie elementarne Δ R jest równa zeru, a praca siły tarcia jest dodatnia:

\(~A_(tr) = F_(tr) \cdot s_(12)\) ,

Przykład 1. Niech siła zewnętrzna F działa na blok W, który można przesuwać na wózku D(ryc. 5). Jeśli wózek przesunie się w prawo, wówczas praca wykonana przez siłę tarcia ślizgowego F tr2 działający na wózek od strony bloku jest dodatni:

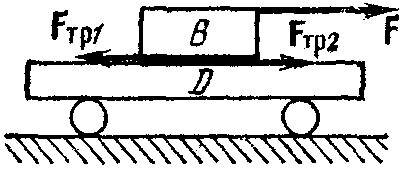
Przykład 2. Kiedy koło się toczy, jego siła tarcia tocznego skierowana jest wzdłuż ruchu, ponieważ punkt styku koła z powierzchnią poziomą porusza się w kierunku przeciwnym do kierunku ruchu koła, a praca siły tarcia jest dodatnia (ryc. 6):

Literatura

Kabardin O.F. Fizyka: Odniesienie. materiały: podręcznik. podręcznik dla studentów. – M.: Edukacja, 1991. – 367 s.
Kikoin I.K., Kikoin A.K. Fizyka: Podręcznik. dla 9 klasy. średnio szkoła – M.: Prosveshchenie, 1992. – 191 s.
Podręcznik do fizyki elementarnej: Proc. dodatek. W 3 tomach / wyd. G.S. Landsberg: tom 1. Mechanika. Ciepło. Fizyka molekularna. – M.: Fizmatlit, 2004. – 608 s.
Yavorsky B.M., Seleznev Yu.A. Podręcznik informacyjny po fizyce dla osób rozpoczynających naukę na uniwersytetach i samokształceniu. – M.: Nauka, 1983. – 383 s.